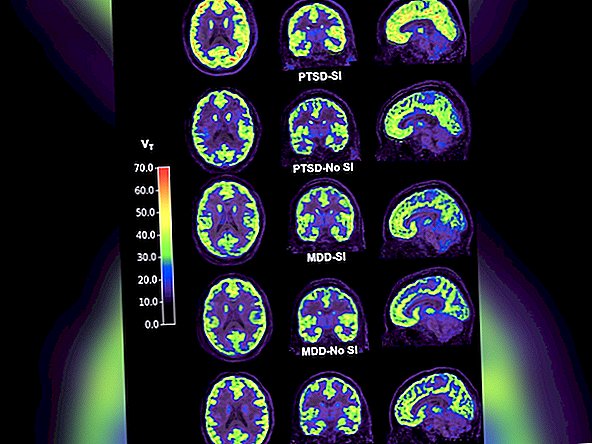
Надпис: Изглед на луната в перигей и апогей
Като преподавател, аз винаги гледам лаборатории с прости настройки, подходящи за студенти. Сегашният ми любим е намирането на скоростта на светлината с шоколад.
В нова книга, наскоро качена в arXiv, Кевин Крисчиунас от Тексас A&M описва метод за определяне на орбиталния ексцентриситет на Луната с изненадващо ниска грешка, използвайки не повече от метър пръчка, парче картон и програма, предназначена за поставяне на криви към променливи звезди.
Този метод използва факта, че ексцентричността може да се определи от съотношението на средния ъглов размер на даден предмет и половината от неговата амплитуда. По този начин основната цел е измерването на тези две количества.
Стратегията на Кевин за това е да използва картонно зрително отворче, което може да се плъзне по метрова пръчка. Като надникнете през дупката на Луната и плъзнете картата напред и назад, докато ъгловият размер на дупката просто се припокрива с луната. Оттам диаметърът на отвора, разделен на разстоянието надолу на метровата пръчка, дава ъгловия размер благодарение на формулата на малкия ъгъл (? = D / D в радиани, ако D >> d).
За да предотвратите систематични грешки при неправилно преценяване, тъй като картата се плъзга напред, докато размерът на дупката съвпада с луната, най-добре е също така да я приближите от другата посока; Влизане от далечния край на пръчката на метъра. Това би трябвало да помогне за намаляване на грешките и при опита на Кевин той откри, че той има типично разпространение от ± 4 мм, когато прави това.
На този етап все още има друга систематична грешка, която трябва да се вземе предвид: зеницата има ограничен размер, съпоставим с мерната дупка. Това ще доведе до подценяване на действителния ъглов размер. Като такъв е необходим коригиращ фактор.
За да изведе този корекционен коефициент, Кевин постави диск от 91 мм на разстояние 10 метра (това трябва да произведе диск със същия ъглов размер като луната, когато се гледа от това разстояние). За да се получи най-доброто съвпадение, плъзгането на картон с мерната дупка Трябва трябва да се постави на метровата пръчка на 681,3 мм, но поради системната грешка на зеницата, Кевин установи, че е необходимо да се постави на 821 мм. Съотношението на наблюдаваното разположение спрямо правилното разположение, при условие че е използван коригиращият коефициент Кевин (1.205). Това трябва да бъде калибрирано за всеки отделен човек и също ще зависи от количеството светлина по време на наблюдението, тъй като това се отразява и на диаметъра на зеницата. Приемането на единен коригиращ фактор обаче дава задоволителни резултати.
Това дава възможност за правилно взети данни, които след това могат да бъдат използвани за определяне на необходимите количества (средния ъглов размер и 1/2 амплитуда). За да ги определи, Кевин използва програма, известна като PERDET, която е предназначена за поставяне на синусоидни криви към трептения в променливи звезди. Всяка програма, която би могла да приспособи такива криви към точките с данни с помощта на?2 годни или анализът на Фурие би бил подходящ за тази цел.
От такива програми, след като се определят средният ъглов размер и половината амплитуда, съотношението им осигурява ексцентричността. За експеримента на Кевин той намери стойност 0,039 ± 0,006. Освен това периодът, който той определя от перигей до перигей, е 27,24 ± 0,29 дни, което е в пълно съгласие с приетата стойност от 27,55 дни.